Pythonの代表的な機械学習ライブラリであるscikit-learnを用いて教師あり学習の回帰と分類を実装し、実際にデータから関数を学習していきます。
Scikit-learnとは
scikit-learnは、オープンソースの機械学習ライブラリで、機械学習の基本的な教師あり学習手法(分類、回帰、モデル選択など)、および教師無し学習手法(クラスタリング、次元削減など)とともに、機械学習に必要とされる汎用的なデータ前処理や評価の機能を提供します。PythonのNumpyなどと連携するように設計されており、使いやすさと実用性とを兼ね備えているため、非常に人気のライブラリです。

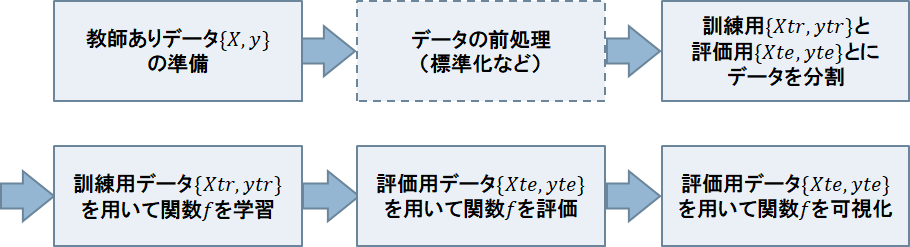
教師あり学習のフロー
教師あり学習のプログラムを一般的なフローは以下のようになります。
以下、物件価格データの敷地面積LotAreaを入力とし、販売価格SalePriceの回帰を例にフローを説明していきます。
一つ一つjupyter notebookでコードを入力し、実行結果をみながら確認していきましょう。

教師ありデータの準備
まず、入力と出力
の対のデータを準備します。
以下のようにデータをpandas.DataFrameに読み込みXとyに代入します。
import pandas as pd data = pd.read_csv('house_prices_train.csv') # DataFrameの読み込み data = data[data['MSSubClass'] == 20] # 建物の等級MSSubClassを20(1階建て、1946年以降)に限定 X=data[['LotArea']].values # 入力データ y=data['SalePrice'].values # 出力データ
データの前処理
入力データが複数ある場合、 データの値の大きさ(スケール)を揃える必要があります。一般的には、標準化と呼ばれる以下のような式で、データの平均が0で、標準偏差が1になるようにデータのスケールを揃えます。
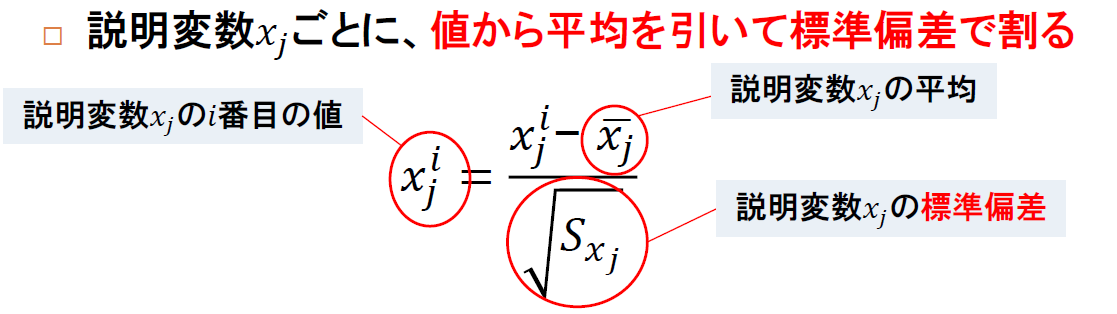
以下のように、numpyを用いると簡単に標準化できます。
Xmean = np.mean(X,axis=0) # 平均 Xstd = np.std(X,axis=0) # 標準偏差 Xnorm=(X - Xmean)/Xstd # 標準化 print(np.mean(Xnorm)) print(np.std(Xnorm)
5.96537744574711e-17 # 標準化後の平均(ほぼ0) 0.9999999999999999 #標準化後の標準偏差(ほぼ1)
訓練用と評価用とに教師データを分割
ランダムまたは何らかの運用上のルール(例えば、期間)に従い、教師データを、訓練用
と評価用
とに分けます。
データの分割には、scikit-learnのtrain_test_splitを用いると便利です。train_test_splitを用いると、ランダムに指定された割合で教師データを訓練用と評価用とに分割してくれます。以下は、80%を訓練用、残りの20%を評価用にランダムに分割する例です。
from sklearn.model_selection import train_test_split Xtr, Xte, ytr, yte = train_test_split(Xnorm, y, train_size = 0.8, test_size = 0.2) # 訓練用と評価用とに分割 print(len(Xtr)) print(len(Xte))
428 # 訓練用データの数 108 # 評価用データの数
関数の学習
訓練用データを用いて、入力から出力の数値を回帰する関数を学習していきます。
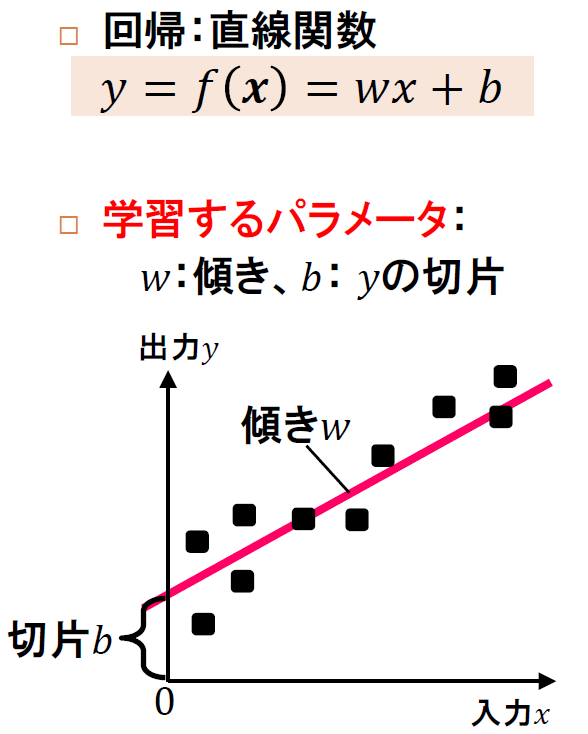
scikit-learnでは、回帰手法として、以下のように直線の関数で入力から出力
を予測する線形回帰LinearRegressionを提供しています。
以下は、LinearRegressionを用いて関数fを定義した後、fitメソッドを用いて訓練用データに対する予測誤差を最小化するように関数fのパラメータを学習します。
from sklearn import linear_model f = linear_model.LinearRegression() # 関数fの定義 f.fit(Xtr, ytr) # 関数fの学習
学習により得られた傾きと切片のパラメータは、以下のcoef_(傾き)、intercept_(切片)を用いて確認することができます。
print(f.coef_) # 傾き print(f.intercept_) # 切片
[16612.13317711] # 傾き 186474.55561352475 # 切片
販売価格SalePriceのy軸に、約18万ドル(=約1900万円)のころで交わり、敷地面積LotAreaが1フィート(=0.3048メートル)平方増加するたびに1万6千ドル(=約180万円)価格が増加するように直線が引かれていることがわかります。
関数の評価
学習した関数fの精度を評価するために、評価データを用います。
以下のように、LinearRegressionのpredictメソッドを用いてに対する予測
を取得します。
ypre = f.predict(Xte)
そして、真の値との誤差を計算します。今回は平均絶対誤差を用います。
print("評価データの絶対誤差=", np.mean(np.abs(yte - ypre)))
評価データの絶対誤差= 55854.1884793132
予測誤差は、平均で約5万ドル(=約550万円)ほどあることがわかります。
可視化
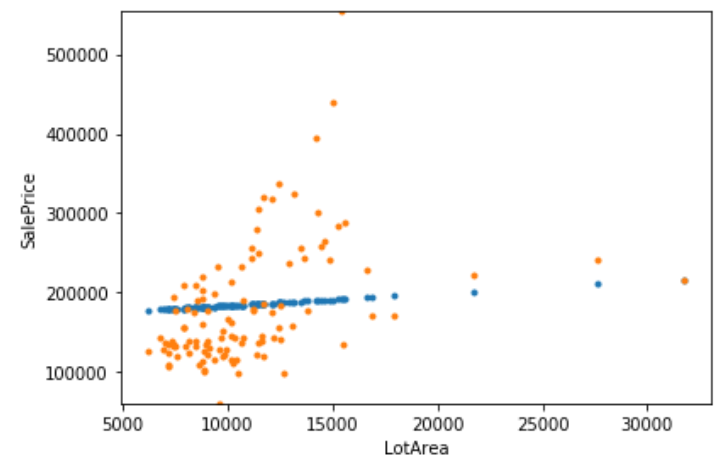
平均的な誤差では実際には、どれくらい予測ができているのか直感的につかめません。そこで、グラフを用いて結果を可視化していきます。
まず、標準化した入力データを、逆の計算を行い、元のスケールに戻します。
Xtmp = (Xte * Xstd) + Xmean
そして、matplotlibのplotを用いて、予測値yprと真値yteの散布図をプロットします。
fig = plt.figure() ax=fig.add_subplot(1,1,1) # 予測のプロット ax.plot(Xtmp, ypre,'.',label='predict') # 真値のプロット ax.plot(Xtmp, yte,'.',label='true') ax.set_ylim([np.min(yte), np.max(yte)]) # y軸の範囲 ax.set_xlabel("LotArea") # x軸のラベル ax.set_ylabel("SalePrice") # y軸のラベル plt.tight_layout() # グラフ間にすきまをあける plt.show() # グラフの表示