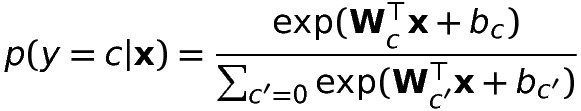<< Pythonによる機械学習1(Pythonの基礎 1/4)
【Pythonによる機械学習1(Pythonの基礎 2/4)の目次】
数値演算のスクリプトの例
以下は、数値計算用のライブライnumpyを用いた線形代数の行列演算を実行するスクリプトの例です。
具体的には、3x3の行列W、Hおよび3次元の列ベクトルx、bに対して、
1) 逆行列、転置行列、行列とベクトルの掛け算および足し算:
![]()
2) 行ベクトルと列ベクトルの掛け算
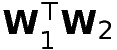
W_iは、行列Wのi列目のベクトル表します
3) 列ベクトルと行ベクトルの掛け算

4) pythonの標準の演算子を用いたアダマール積(要素ごとの積):
![]()
を計算しています。
# -*- coding: utf-8 -*- # 数値計算用のライブラリnumpyをnpとしてインポート import numpy as np import pdb # 3x3のnumpy配列(行列) W = np.array([ [1,0,0], [0,1/2,0], [0,0,1/3] ]) H = np.array([ [1,0,0], [0,2,0], [0,0,3] ]) print(f"W:\n{W}\nH:\n{H}\n") # 3x1のnumpy配列(ベクトル) x = np.array([ [1], [2], [3] ]) b = np.array([ [1], [2], [3] ]) print(f"x:\n{x}\nb:\n{b}\n") # 逆行列の計算 W_inv = np.linalg.inv(W) print(f"W_inv:\n{W_inv}\n") # 行列W_invの転置とベクトルxの掛け算とbとの足し算 W_inv_transpose = W_inv.T f_x = np.matmul(W_inv_transpose,x) f_x = f_x + b print(f"W_inv_transpose:\n{W_inv_transpose}\n") print(f"f_x:\n{f_x}\n") # Wの1列目の転置 row1W = W[:,[0]].T # Wの2列目 col2W = W[:,[1]] print(f"1st row of W:\n{row1W}\n2nd colmn of W:\n{col2W}\n") # 行ベクトルと列ベクトルの掛け算 rowXcol = np.matmul(row1W,col2W) print(f"row x col vectors:\n{rowXcol}\n") # 列ベクトルと行ベクトルの掛け算 colXrow = np.matmul(col2W,row1W) print(f"col x row vectors:\n{colXrow}\n") # 行列のアダマール(要素ごとの積)積 g_H = W*H print("g(H):\n{}\n".format(g_H))
上記のスクリプトをファイルlinearAlgebra.pyに保存し以下のように実行します。
> python linearAlgebra.py W: [[ 1. 0. 0. ] [ 0. 0.5 0. ] [ 0. 0. 0.33333333]] H: [[1 0 0] [0 2 0] [0 0 3]] x: [[1] [2] [3]] b: [[1] [2] [3]] W_inv: [[ 1. 0. 0.] [ 0. 2. 0.] [ 0. 0. 3.]] W_inv_transpose: [[ 1. 0. 0.] [ 0. 2. 0.] [ 0. 0. 3.]] f_x: [[ 2.] [ 6.] [ 12.]] 1st row of W: [ 1. 0. 0.] 2nd colmn of W: [[ 0. ] [ 0.5] [ 0. ]] row x col vectors: [ 0.] col x row vectors: [[ 0. 0. 0. ] [ 0.5 0. 0. ] [ 0. 0. 0. ]] g_x: [[ 1. 0. 0.] [ 0. 1. 0.] [ 0. 0. 1.]]
numpy.ndarray.Tは行列の転置、numpy.matmulは行列・ベクトルの掛け算を返します。詳細は、以下を参照してください。
https://docs.scipy.org/doc/numpy-1.13.0/reference/generated/numpy.ndarray.T.html
https://docs.scipy.org/doc/numpy-1.13.0/reference/generated/numpy.matmul.html
pdbを用いたデバッグ
以下のように、pdbモジュールをインポートし、スクリプトの任意の行に「pdb.set_trace()」を設置すると、その処理を止めて、途中経過を確認することができます。
# デバッガをインポート import pdb pdb.set_trace()
スクリプトlinearAlgebra.pyの17行目に「pdb.set_trace()」を設置し、実行してみましょう。
16 # 逆行列の計算 17 pdb.set_trace() 18 W_inv = np.linalg.inv(W) 19 print("W_inv:\n{}\n".format(W_inv))
> python linearAlgebra.py > /home/staff/hhachiya/Works/intelligentSystemTraining/linearAlgebra.py(19)<module>() -> W_inv = np.linalg.inv(W) (Pdb)
pdb.set_trace()をで処理が「l」を入力し、Enterを押すと、現在実行中のコードを表示できます。
(Pdb) l
14 b = np.array([ [1], [2], [3] ])
15 print("x:\n{}\nb:\n{}\n".format(x,b))
16
17 # 逆行列の計算
18 pdb.set_trace()
19 -> W_inv = np.linalg.inv(W)
20 print("W_inv:\n{}\n".format(W_inv))
21
22 # 行列Wの転置とベクトルxの掛け算とbとの足し算
23 W_inv_transpose = W_inv.T
24 f_x = np.matmul(W_inv_transpose,x)
(Pdb) 次に、変数名「W」を入力し、Enterを押すことにより、処理途中の変数f_xの値を表示できます。
(Pdb) W
array([[ 1. , 0. , 0. ],
[ 0. , 0.5 , 0. ],
[ 0. , 0. , 0.33333333]])
(Pdb)現在の行を実行するために「n」を入力し、Enterを押します。そして、「W_inv」を入力し、Enterを押すと更新された変数f_xの値を表示できます。
(Pdb) n
> /home/staff/hhachiya/Works/intelligentSystemTraining/linearAlgebra.py(20)<module>()
-> print("W_inv:\n{}\n".format(W_inv))
(Pdb) W_inv
array([[ 1., 0., 0.],
[ 0., 2., 0.],
[ 0., 0., 3.]])最後に「c」を入力し、Enterを押すと終了(実際には次のpdb.set_trace()まで実行)します。
このように、任意の行で処理を止めて、処理途中の変数の値を確認したり、新たな処理を試したりすることが出来るので、効率よく実装ができます。
演習2
次の行列Aを定義し、その逆行列A^-1および行列Aと逆行列A^-1の積を計算し出力してみましょう。
作成したスクリプトおよび出力結果を、Moodleにて提出してください。
宿題1
指数関数numpy.expと、和を求める関数numpy.sumを使って、ソフトマックスの計算をlinearAlgebra.pyに追加してみましょう。
ここで、W_iは行列Wのi列のベクトルを意味します。
また、b_iはベクトルbのi番目の要素(スカラー)を意味します。
numpy.expとnumpy.sumの詳細については以下を参照してください。
https://docs.scipy.org/doc/numpy-1.13.0/reference/generated/numpy.exp.html
https://docs.scipy.org/doc/numpy-1.13.0/reference/generated/numpy.sum.htmlまた、行列W、ベクトルxおよびbは、linearAlgebra.pyにて既に設定されているものを利用してください。
作成したスクリプトおよび出力結果を、次週までにMoodleにて提出してください。