Pythonの数値計算ライブラリNumpyを使って行列演算をしてみた。まずは、Numpyをインポートする。
import numpy
次に、arrayを使ってベクトルa, b, cを定義する。
次に、ベクトルの転置とベクトルの積から行列A, B, Cを計算する。
A=a.T*a
B=b.T*b
C=c.T*c
つまり、a.T、b.T及びc.Tは、それぞれベクトルa, b及びcの転置である。
行列Aを表示してみると、3x3の行列になっている。
>>> A
array([[1, 2, 3],
[2, 4, 6],
[3, 6, 9]])
次に、行列A, B及びCのランクを見てみる。
>>> linalg.matrix_rank(A)
1
>>> linalg.matrix_rank(B)
1
>>> linalg.matrix_rank(C)
1
行列のサイズは3x3だが、ベクトルの転置とベクトルの掛け算による行列は、その行及び列を元のベクトルをただ定数倍して並べただけなので、ランクは1しかないことがわかる。したがって、当然ながらランク落ちにより、逆行列は計算できず、次のようなエラー「Singular matrix」がでる。
>>> linalg.inv(A)
Traceback (most recent call last):
File "", line 1, in
File "C:\Anaconda\lib\site-packages\numpy\linalg\linalg.py", line 520, in inv
ainv = _umath_linalg.inv(a, signature=signature, extobj=extobj)
File "C:\Anaconda\lib\site-packages\numpy\linalg\linalg.py", line 90, in _raise_linalgerror_singular
raise LinAlgError("Singular matrix")
numpy.linalg.linalg.LinAlgError: Singular matrix
行列のランクを上げるために、3つの行列を足してみる。
D=A+B+C
D
>>> D
array([[42, 57, 42],
[57, 78, 57],
[42, 57, 54]])
>>> linalg.matrix_rank(D)
3
これで無事行列のランクが3と行列のサイズと等しくなったので、これの逆行列を計算してみる。
>>> linalg.inv(D)
array([[ 2.97222222e+00, -2.11111111e+00, -8.33333333e-02],
[ -2.11111111e+00, 1.55555556e+00, -0.00000000e+00],
[ -8.33333333e-02, -9.25185854e-18, 8.33333333e-02]])
今回はエラーが出ずに逆行列が得られた。
>>> linalg.eig(A)
(array([ 1.40000000e+01, 3.58824538e-16, -5.87239501e-16]), array([[ 0.26726124, -0.11336834, 0.6357427 ],
[ 0.53452248, -0.80883073, -0.72308631],
[ 0.80178373, 0.57700993, 0.27014331]]))
>>> W, V=linalg.eig(A)
>>> W
array([ 1.40000000e+01, 3.58824538e-16, -5.87239501e-16])
>>> V
array([[ 0.26726124, -0.11336834, 0.6357427 ],
[ 0.53452248, -0.80883073, -0.72308631],
[ 0.80178373, 0.57700993, 0.27014331]])
>>> W, V=linalg.eig(D)
>>> W
array([ 164.9548855 , 0.22263275, 8.82248175])
>>> V
array([[ 0.49879555, 0.8118207 , -0.30356244],
[ 0.67958527, -0.5837051 , -0.44435595],
[ 0.5379283 , -0.0153462 , 0.8428509 ]])
行列Aはランクが1のため、固有値も一つだけ正の値を取り、残り2つは、10^-16とほぼ0であることがわかる。
一方、行列Dはランクが3のため、固有値は3つとも正の値をとっていることがわかる。
次に、固有値分解をしてみる。
>>> A+B
array([[17, 22, 27],
[22, 29, 36],
[27, 36, 45]])
>>> linalg.matrix_rank(A+B)
2
>>> W,V=linalg.eig(A+B)
>>> W[0]*dot(V[:,0:1],V[:,0:1].T) + W[1]*dot(V[:,1:2],V[:,1:2].T)
array([[ 17., 22., 27.],
[ 22., 29., 36.],
[ 27., 36., 45.]])
行列A+Bのランクは2なので、2つの固有値W[0:2]と固有ベクトルV[:,0:2]を使って、近似できているのがわかる。
ここで使っている固有値分解は、次の式で表される。
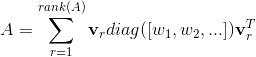
つまり、w_rとv_rは、r番目の固有値と、固有ベクトルであり、diag([w_1,w_2,...])は、対角成分にw_1, w_2, ...を持つ対角行列である。
これを行列表現すると、次のようになる。

Pythonで、実装すると次のようになる。
>>> dot(dot(V,diag(W)),V.T)
array([[ 17., 22., 27.],
[ 22., 29., 36.],
[ 27., 36., 45.]])
Numpyの行列演算は、普段Matlabを使っているため少し不便さを感じる所はあるが、慣れれば問題なさそうである。